Napier and the logarithms
John Napier, by discovering logarithms, revolutionized scientific computing.
Logarithms remained in use for over 300 years, enabling precise astronomical and scientific calculations.
The mathematician John Napier discovered in 1614 the logarithms, published in "Mirifici logarithmorum canonis descriptio", capable of expressing any positive number via powers.
Since the product of two powers with the same base is a power with the same base and exponent given by the sum of the exponents, with logarithms multiplications and divisions can be made as simple additions and subtractions.
To multiply two numbers just look out for their logarithms and add them together: the result is the number whose logarithm correspond to the sum.
In practice the logarithm of a number in a certain base is the exponent to which the base must be raised to obtain the number.
The logarithm of 10,000 in base 10 is 4 (104 = 10,000) and 10,000 x 1,000 become 104x103 = 104+3 = 107 = 10,000,000.
Multiplication and division of exponents allow to find squares, cubes and roots. Things get complicated when dealing numbers other than 10: we need a volume with more than a million values.
The tables had a very long life as they were cheap and their precision made them indispensable for astronomers and navigators ap to ca 1975.

Table from "Mirifici logarithmorum canonis descriptio", 1614
How to calculate with logarithms
Calculating with logarithms is a mechanical process that doesn't engage the mind, but using the tables requires a lot of practice. Let's try 10.34 x 1,347. First, we need to find the logarithm of 10.34. The table gives us only the decimal part of the logarithm (mantissa). The whole part is given by the power of ten of the number, so 1.
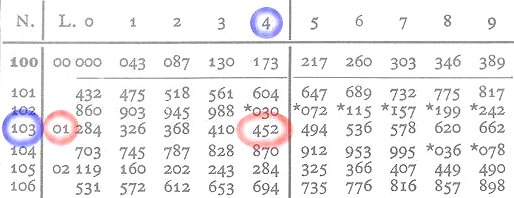
To find the decimal part, we remove the decimal point from the number, which becomes 1034. Column N indicates the first three digits. The fourth digit will be in the columns numbered 0 through 9.
The first two digits of the decimal part are in column L, corresponding to the 103 of column N (01). The other three digits are on the same row in the 4 column (452). The decimal part will therefore be 01452. The complete logarithm is 1.01452.
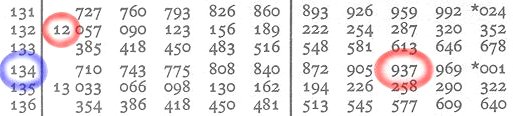
Now, in the same way, we'll hunt for the logarithm of 1,347. The whole number is 3 (10 x 10 x 10 = 1,000) and the first 3 digits are 134. On line 134, the value in column L is missing, so we'll take the last value before line 134 (12). The other 3 are on line 134 of N in column 7 (937). The decimal number will therefore be 12,937. The full logarithm is 3.12,937.
Now add the logarithm of 10.34 to the logarithm of 1.347 (for division, subtract): 1.01452 + 3.12937 = 4.14389. The product of 10.34 and 1.347 will be the number whose logarithm is 4.14389; look it up in the tables.
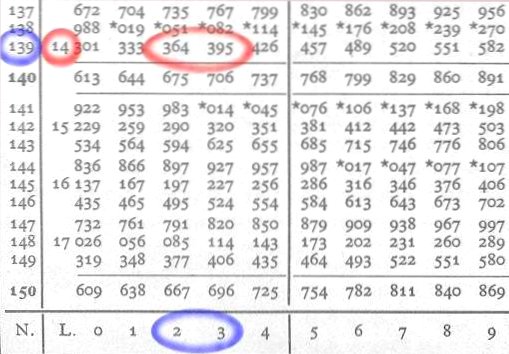
The whole part of the logarithm is the power of 10 of the number we are looking for (4). With the decimal part (14389) we will find the other digits.
The decimal portion begins with the 2 digits (14), which we find in column L and then look for the other 3 digits (389) in the following columns numbered from 0 to 9. 389 is missing, but there are 364 in column 2 and 395 in column 3 of row 139 of N. The result will be approximately between 13,920 and 13,930.
To obtain the exact fifth digit we will interpolate with the P.P. (partes proportionales) multiplication tables.
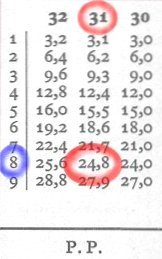
First we need to find the difference between 395 and 364 (the two numbers in columns 2 and 3) 395 - 364 = 31 and we will consult the P.P. table in column 31. Then we will look for the difference between 389 (the value not found) and 364 (the smaller of the two found). 389 - 364 = 25 looking in column 31 for the value closest to 25 (24.8). In the first column, corresponding to 24.8, we find the number 8 and the exact result will be 13,928. In fact, 10.34 x 1,347 = 13,928.
Today it seems an impractical system, but Napier wrote: "I have tried, using all the means at my disposal and with the strength of my intellect, to make the calculation easier and quicker by developing the method of logarithms, to which I have devoted many years of study."
A goal achieved, and 200 years later Pierre-Simon de Laplace stated that "Napier's work has doubled the life of us astronomers."
Links:
© 2004 - 2026 Nicola Marras Manfredi - IS1EH
