Storia del regolo calcolatore

Il regolo calcolatore era l'unico strumento utilizzato per progettare fino al 1970 circa.

Il regolo calcolatore, o Slide Rule, sostituisce le funzioni matematiche con misurazioni lineari: moltiplicazioni e divisioni sono alla portata di tutti.

Qui una breve storia e tutorial del regolo calcolatore, la versione completa è scaricabile gratuitamente. Il funzionamento è illustrato in questa sezione.

"Houston, Tranquility Base here: The Eagle has landed".

così Armstrong annunciava il 20 luglio 1969 l'atterraggio sulla Luna. Uno dei calcolatori di bordo era un regolo calcolatore tascabile, in dotazione a tutte le missioni Apollo.
Inventato nel 1600 questo strumento arrivò nello spazio. Una storia ormai dimenticata, superata da un'era digitale che sembra esistere da sempre.

Regolo calcolatore Pickett N600 ES, adottato dalla NASA

INTEL 4004, il primo microprocessore, fu disegnato da Federico Faggin nel 1971.
Al tempo i computer erano enormi e necessitavano di un operatore, per accedervi bisognava prenotare con anticipo.

Si progettava tutto coi regoli calcolatori, eventualmente chiedendo verifica al computer solo a fine lavoro.
Il calcolo strutturale di aeroplani, mezzi spaziali ecc. necessitava ormai di una precisione assoluta. Si utilizzavano regoli circolari, le cui lunghe scale garantivano risultati esatti.

1971: regolo Gilson e processore 4004 firmato da Faggin

Nel 1971 il 4004 venne montato su una ingombrante calcolatrice Busicom, ma già l'anno successivo apparve la HP 35, prima calcolatrice scientifica portatile. L'era dei regoli calcolatori era finita, vediamola brevemente.

Gli esordi del regolo calcolatore

Nel 1617 John Napier rivoluzionò la matematica scoprendo i logaritmi. Si potevano finalmente eseguire con relativa rapidità calcoli complessi.

Nel 1620 Edmund Gunter disegnò la scala logaritmica posizionando i numeri su di un righello ad una distanza dall'origine proporzionale al valore del loro logaritmo.
Invece di cercare i logaritmi nelle tavole basta addizionarli con l'aiuto di un compasso.

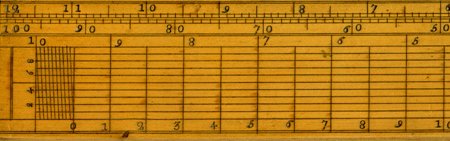
Particolare di un righello di Gunter, ca. 1790

Questo strumento rimase in uso fino agli inizi del '900, nonostante il regolo calcolatore fosse stato inventato già nel 1622. In quell'anno infatti William Oughtred duplicò le scale logaritmiche facendole scorrere parallelamente. Un innovazione che permette la lettura rapida e diretta del risultato.

Nel 1654 Robert Bissaker marcò le scale su più righelli scorrevoli.
Chiamato Gauging Rule questo regolo era specializzato nel misurare il contenuto dei barili di vino, birra o liquori e calcolarne il carico fiscale.

Regolo fiscale Everard, ca. 1780

Nel 1677 Hery Coggeshall creò la Carpenter's Slide Rule, montata su due righelli di legno con la gradazione in pollici, la scala centrale scorrevole in bronzo e diverse altre scale per la risoluzione di vari problemi.
E' uno strumento che ha permesso di misurare e calcolare anche alla gente comune, utilizzato fino al' 900 nei cantieri navali e nelle carpenterie.

Carpenter's Rule, ca. 1850

All'inizio del 1700 esistevano quindi regoli specifici per gli usi dell'epoca: la Carpenter's Slide Rule trovava il volume ed il peso dei carichi di legname.
La Gauging Rule calcolava la tassazione delle botti di birra e la Gunter's Scale permise la mappatura degli Stati Uniti.

Gauging Rule, ca. 1820

Verso metà '800 ci fu l'esigenza di strumenti di calcolo non solo destinati all' uso fiscale o marittimo.
Indispensabili per progettare macchine a vapore e ferrovie, apparvero regoli calcolatori per ogni uso, armi segrete della rivoluzione industriale. Al fine di migliorarne la precisione, proporzionale alla lunghezza delle scale, si produssero modelli circolari.

Charpentier, tascabile: ca. 1880, uno dei primi regoli generici

L'età d'oro

Nel 1859 il tenente di artiglieria francese Amedeè Mannheim migliorò le scale introducendo il cursore mobile.
Era nato il regolo calcolatore moderno, introdotto in Italia da Quintino Sella.

Uno dei primi cursori "Mannheim", fine '800

Cursore del Faber Castell, ca. 1930

Regolo calcolatore Nestler 23, il preferito a Einstein, ca. 1930

Attorno al 1920 il regolo calcolatore aveva assunto la sua forma definitiva. Einstein lo utilizzò per elaborare la teoria della relatività, Fermi per la bomba atomica, Korolev per il programma Sputnik e Von Braun per i motori del Saturno V, il vettore lunare.

Modelli circolari Fowlers, ca. 1910

Nel 1878 George Fuller brevettò una precisissima "Elica Calcolatoria" cilindrica con ben 13 metri di scala. Rimasta in commercio fino al 1972, servì per progettare dirigibili, aeroplani, ponti e grattacieli.

Modello cilindrico Fuller, 1921

Il regolo calcolatore cilindrico veniva prodotto anche in versione tascabile. Alcuni erano inseriti come manici nei bastoni: un idea per l'iPhone!

Modello cilindrico inserito in un bastone da passeggio, 1926

I numeri complessi, scoperti da Rafael Bombelli alla fine del '500, furono poi sviluppati nel '700 da Gauss, Ruffini e Abel.
Un numero si dice complesso quando e' formato da un numero reale e da uno immaginario (Es: 3+2i).

Regolo calcolatore con scala per numeri complessi, ca. 1952

Oggi sembra impossibile risolvere equazioni composte da numeri complessi senza computer, ma esistevano modelli di regolo calcolatore con scale specifiche.
La meccanica quantistica si è potuta sviluppare anche grazie ad essi.

Grande regolo cilindrico, ca. 1936

Il regolo calcolatore in guerra

Il regolo moderno fu realizzato dal tenente francese Amedè Mannheim per massimizzare il tiro dei suoi cannoni.
Il regolo è ancora in forza negli eserciti: quale calcolatore potete lasciare acceso senza mai sostituirne le batterie o lanciare da 50 metri utilizzandolo poi senza problemi? Infine, durante la guerra fredda, si temeva un attacco nucleare e solo il regolo può funzionare in ambienti contaminati.
In situazioni critiche l' affidabilità è essenziale.

Regoli per misurare l'esposizione alle radiazioni e da tiratore scelto

I regoli calcolatori servirono agli artiglieri per risolvere il triangolo di tiro.
Vennero usati anche in meteorologia per analizzare i dati forniti dai palloni sonda: le previsioni erano essenziali nella pianificazione degli attacchi ed anche la data del "D-Day" venne scelta in base al bollettino del tempo.

Elaborazione del bollettino meteorologico

Il lancio dei siluri necessita di molti calcoli. Italiani e tedeschi avevano solo un regolo circolare, gli Americani regoli elettromeccanici che trovavano automaticamente la miglior soluzione di tiro.
Coraggio e audacia niente poterono contro questa superiore tecnologia e tanti nostri sommergibili non rientrarono alla base.

Regolo calcolatore automatizzato USA e il semplice modello dell'Asse

Le tecniche di bombardamento esigevano una perfezione assoluta nella determinazione dei bersagli, spesso notturni od oscurati dalle nubi, nelle basi a terra i regoli calcolatori erano utilizzati dal personale di supporto tattico per disegnare la mappa delle battaglie aeree.

Calcoli tattici col regolo calcolatore durante la Battaglia d'Inghilterra

Le esigenze della navigazione aerea portarono al regolo aeronautico E6B, che si dimostrò insostituibile. Rimase infatti l'unico calcolatore di bordo fino ai primi Jumbo Jet ed ancora oggi è utilizzato negli aeroplani da turismo. Visitate la sezione dedicata.

Il primo regolo calcolatore E6B, capostipite di una serie ancora in commercio

La fine di un epoca

I primi elaboratori elettronici apparvero verso il 1946 ma erano giganteschi e costosi: il regolo calcolatore sembrava insostituibile. Non si immaginava un mondo senza di loro: servivano alle massaie in cucina, tracciavano le rotte sull'astronave di "Star Trek", apparvero sulla copertina di Playboy.

Elezione di "Miss Regolo Calcolatore", ca. 1950

Ne esistevano di tutti i tipi, in Braille per i non vedenti, con scale dedicate alla risoluzione di problemi statistici, ed anche in base esadecimale, ottale o binaria per i primi programmatori di computer.

Modello in esadecimale per programmatore di computer

Era il laptop dell' epoca, che spuntava immancabilmente dal taschino degli ingegneri. Un vero segno identificativo della categoria.

Nel 1955, dopo 9 anni di prove, venne consegnato uno degli aeromobili più rivoluzionari della storia: il Boeing B52 Stratofortess, bombardiere nucleare a lungo raggio.
Progettato coi regoli calcolatori, ha una struttura ad ala flessibile moderna e innovativa. Prodotto fino al 1962 è così ben concepito da essere ancora in servizio, aggiornato nell'elettronica.
La sua dismissione è infatti prevista per il 2040.

Il jet B52 e il regolo calcolatore usato dalla Boeing

I regoli calcolatori sono precisi fino al terzo decimale ed occorre effettuare continue stime. Approssimando per eccesso si creò il mito dei "vecchi oggetti robusti", ma il calcolo strutturale esigeva ormai risultati esatti, favorendo lo sviluppo dei calcolatori elettronici commerciali. Questi furono progettati interamente coi regoli.
Robert Ragen affermava di averne consumati due per realizzare nel '63 il suo rivoluzionario Friden 130, ancora costoso ed ingombrante.

Per migliorare la precisione si progettarono modelli che proiettavano una scala logaritmica virtuale lunga diversi metri, purtroppo molto costosi.

Regolo a proiezione Salmoiraghi, probabilmente
il miglior calcolatore analogico mai costruito

Nel 1969, dopo essere stato indispensabile nella progettazione dei vettori spaziali, il regolo calcolatore venne utilizzato sull'Apollo 11, sbarcando sulla Luna. Una lunga carriera, iniziata più di 350 anni prima, però ...

Inventato nel XVII secolo il nostro strumento è infine arrivato nello spazio

... nel 1972 la Helwett Packard, reclamizzandola come "Innovativo regolo calcolatore elettronico", mise in vendita la prima calcolatrice scientifica economica, 50 volte più piccola delle concorrenti e tanto moderna da essere ancora in commercio.
Le funzionalità della HP-35 erano irrinunciabili, è considerata uno dei 20 oggetti che hanno cambiato il mondo, ed il regolo calcolatore scomparve dal mercato in pochi mesi. Era cominciato il mondo moderno.

Dal 1972 nello spazio solo le nuove Helwett Packard

La HP 35 utilizza il principio logico della notazione polacca inversa (RPN), ideato negli anni '20 da Lukasiewicz, che permette di descrivere qualsiasi formula senza uso di parentesi. Prima si inseriscono gli operandi e poi gli operatori: (4 + 5) x 6 si digita come 4 ENTER 5 + 6 x e quindi manca il tasto = a cui siamo abituati.

Provate la simulazione in Java della HP35, Neil Fraser

Calcolare l'ipotenusa di un triangolo rettangolo coi cateti di 3.4 e 4.3 cm

La RPN si evita i problemi dovuti alle parentesi e alla precedenza degli operatori (prima la divisione, poi l'addizione ecc.). Era finito il tempo di cercare i risultati interpretando le scale.

Gli ultimi regoli calcolatori avevano più di 30 scale

Il calcolo analogico oggi

Gli ultimi regoli calcolatori (Inglese)

Il nostro "eroe", affidabile ed ecologico, è però sempre indispensabile a piloti e militari. Nel romanzo di fantascienza "The feeling of power" di Isaac Asimov si ipotizza un ritorno agli antichi sistemi di calcolo, concludendo con queste parole:

"Nove volte sette - pensò Shuman - fa sessantatrè, e non ho bisogno che me lo venga a dire una calcolatrice. La calcolatrice ce l'ho nella testa. E questo gli dava un senso di potenza davvero esaltante".

I primi calcolatori erano ingombranti e costosi, ma sostituivano 150
ingegneri muniti di regolo calcolatore: il loro tempo era arrivato

Links sul regolo calcolatore:

Il regolo calcolatore su Wikipedia
The Oughtred Society
The Slide Rule Museum
rechenschieber.org
Regoli calcolatori medici

Pubblicità del regolo Pickett: 5 missioni lunari!

© 2004 - 2024 Nicola Marras Manfredi