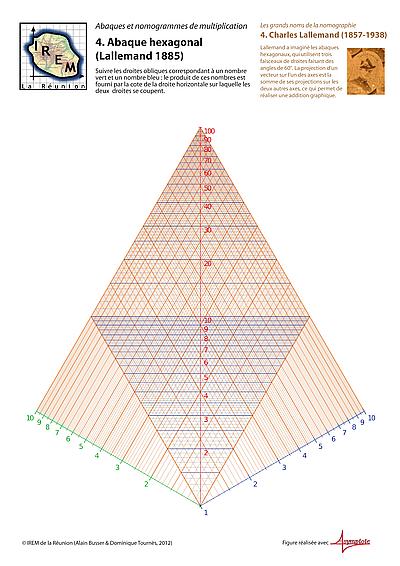
Scaricate il nomogramma con gli esempi di calcolo
Abachi, nomografia, slide chart, volvelle
Nel 1844 Leon Lalanne creò l'Abaque Compteur, introducendo la nomografia.
I nomogrammi e le successive slide chart furono l'equivalente delle moderne app.
Questi semplici calcolatori per usi specifi resero finalmente il calcolo alla portata di tutti.
Abaque e nomogrammi sono in sintesi la rappresentazione grafica dei rapporti matematici. Questo tipo di calcolo, prefigurato da Pouchet nel '700, ebbe la prima applicazione con Lalanne e venne sviluppato da d'Ocagne, che gli diede il nome di nomografia.
Leon Lalanne appese copie del suo Abaque Compteur nelle piazze e nei ritrovi di affari, dando così grande fama al suo metodo. In Francia, dopo la legge del 1842 che pianificava la costruzione della rete ferroviaria, era necessario risolvere rapidamente calcoli complessi.
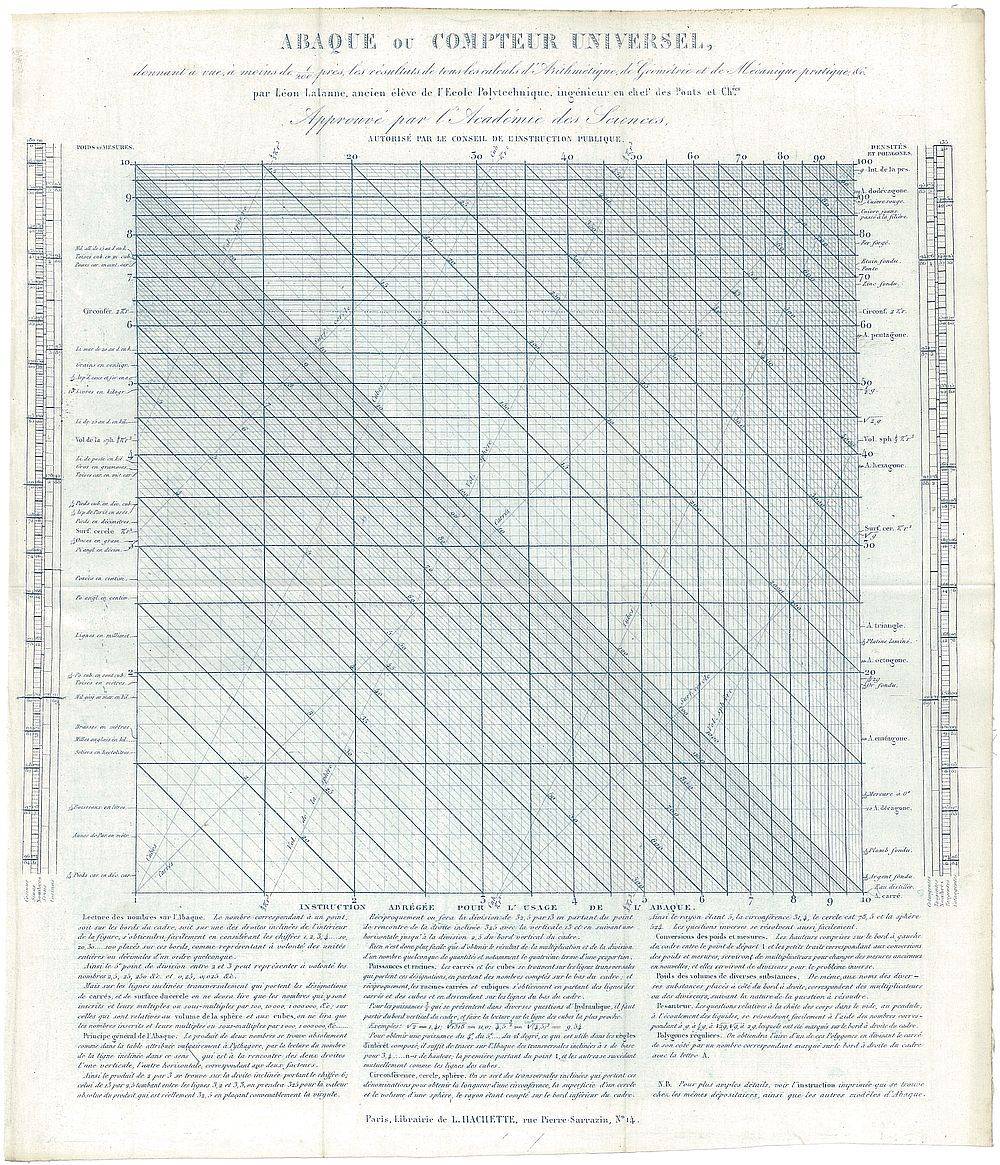
L'Abaque Compteur di Leon Lalanne, ormai quasi introvabile
Calcolare con gli abachi
L'Abaque di Leon Lalanne permette di operare molto rapidamente a scapito di una piccola perdita di precisione.
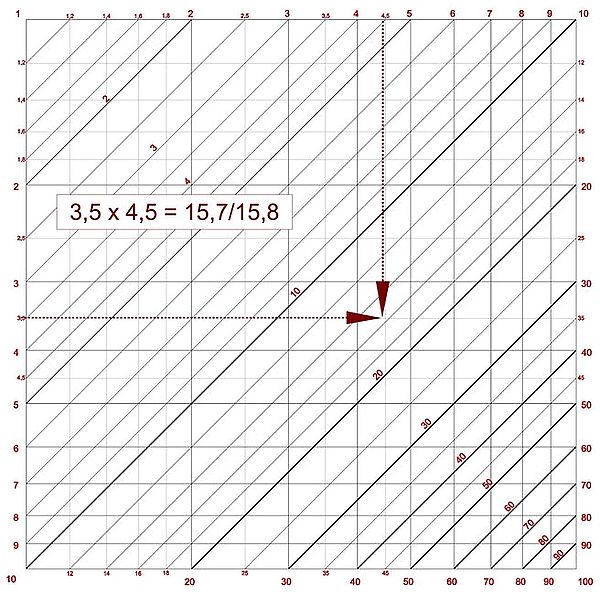
Supponiamo di voler eseguire 3,5 x 4,5: basta cercare l'intersezione dei due valori sulla diagonale e leggere il risultato.
In questo caso l'intersezione è vicino a 16 e possiamo valutare a occhio il risultato in ca. 15,5.
In realtà 3,5 x 4,5 = 15,75 e non 15,5, un errore inferiore al 2%.
Le cose si complicano moltiplicando, per esempio, 172 x 37: bisogna ridurre a 1,72 x 3,5 e poi aggiungere gli zeri al risultato.
Naturalmente è anche possibile dividere.
 .
.
Nonostante siano ancora utilizzati per calcoli specialistici gli abachi non ebbero mai il successo sperato. La storia continua con lo sviluppo della nomografia, ancora più semplice e intuitiva.
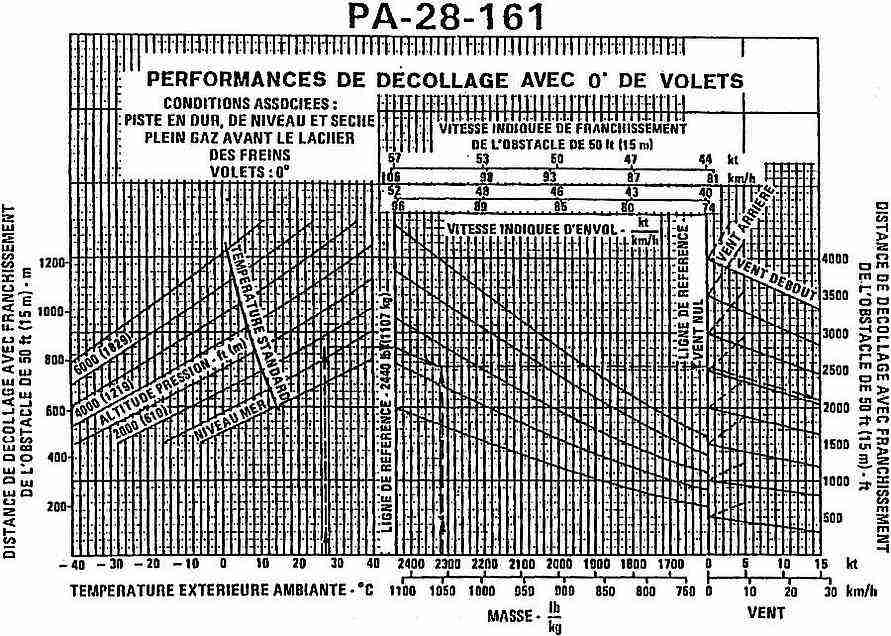
Abaque per la determinazione dello spazio di decollo, 1965
La nomografia è stata inventata nel 1884 da Maurice d'Ocagne, che riprese il lavoro di Lalanne sostituendo le scomode coordinate cartesiane con un sistema di più pratiche scale parallele. Il nome deriva dalle radici greche nomos (legge) e graphein (scrivere).
Il nomogramma nella sua forma più semplice è costituito da tre scale graduate. Nelle due scale esterne si identificano i valori del problema da risolvere e, congiungendoli con una retta, chiamata linea d'indice, si puà leggere il risultato all'incrocio con la scala centrale. Le scale possono essere lineari o logaritmiche.
La nomografia ha permesso a tutti di effettuare calcoli con grande facilità, basta infatti disegnare una o più linee senza nemmeno dover conoscere l'equazione che si sta risolvendo.
Una gran cosa prima che le calcolatrici elettroniche ci semplificassero la vita.
Questo nomogramma è estremamente intuitivo: basta unire con un righello i valori del nostro peso e della nostra altezza per sapere se dobbiamo subito metterci a dieta.

Calcolare coi nomogrammi
I nomogrammi sono strumenti analogici la cui precisione è limitata dall' accuratezza con cui si riescono a stampare e leggere le scale. Trovano ancora oggi largo impiego per usi militari, in medicina ed in aeronautica; spesso inseriti in tabelle scorrevoli, dette slide chart.
Per moltiplicare con il nomogramma congiungete con un righello i due fattori delle scale A e B e leggete il risultato nella scala centrale. Per dividere invertite il procedimento.
Nelle colonne A2 e B3 si leggono quadrati e cubi ed estraggono le radici. In questo esempio la retta rossa esegue 2x5=10 o 10/2=5 o 10/5=2; la blu 6x3=18 o 18/3=6 o 18/6=3.

Divisione dove il numeratore è una radice quadrata √350 ÷ 1,51:
- a fianco del 3,5 della scala A2 troviamo sulla scala A la radice quadrata di 350: 18,7;
 >
>
- adesso colleghiamo il 18,7 della scala AxB col 1,51 della scala A e leggiamo il risultato sulla B: ca. 12,39. Con una calcolatrice saremmo stati solo di poco più precisi, trovando 12,3896.

Questa è una tabella per la determinazione dello spazio di decollo, di utilizzo molto più rapido rispetto al precedente abaque.
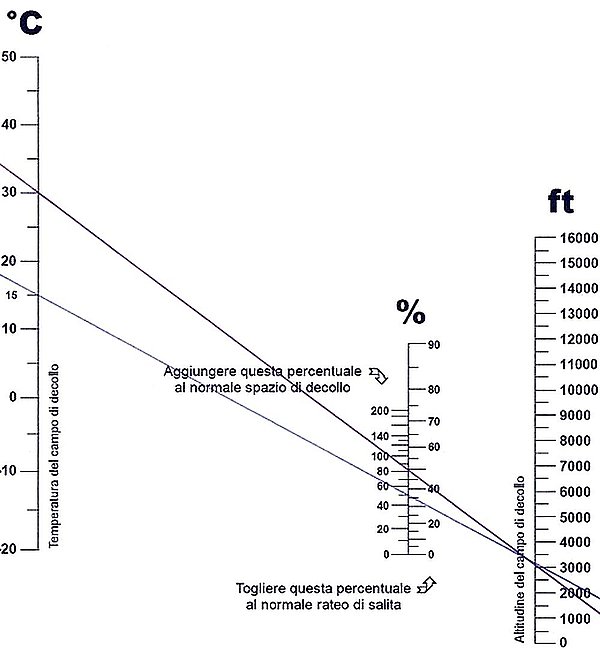
Il manuale indica 500 mt come corsa di decollo in condizioni standard: pista a livello del mare e 15° celsius.
Altitudini e temperature superiori diminuiscono la densità dell'aria, aumentando lo spazio necessario.
Siamo a 900 metri di quota (3000 ft) e 30°: congiungendo temperatura e altitudine rileviamo come ci occorra l'80% in più di pista, 900 mt.
Al mattino con 15° l'aria sarà più densa e basteranno 665 mt.
Ulteriori informazioni nella sezione dedicata ai nomogrammi per elettrotecnici
Le slide chart, o infografiche, sono nomogrammi inseriti in una copertina di cartoncino e programmati per risolvere calcoli specifici. Equivalgono alle moderne app per smartphone e quando sono costruite con forma circolare vengono chiamate Volvelle.

Slide chart per calcolare la resistenza delle travi in legno, 1902
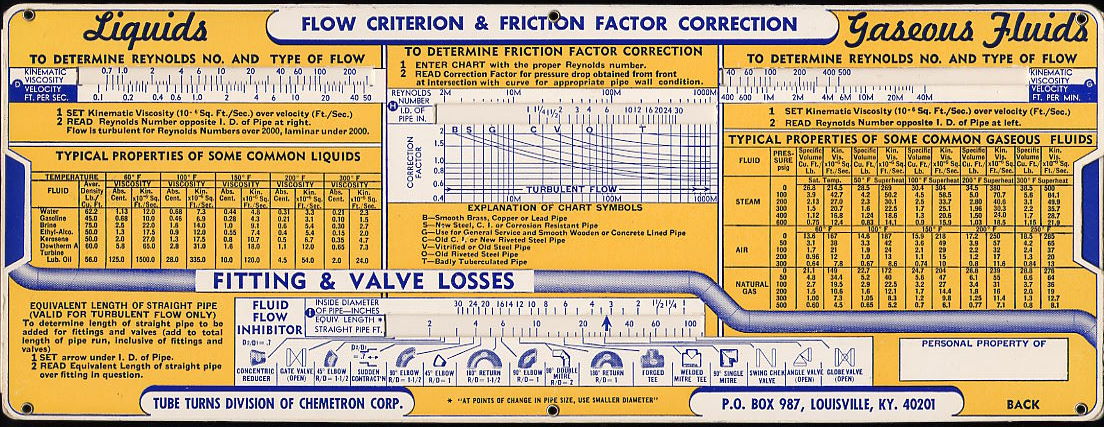
Calcolatore di velocità e perdita di pressione per fluidi, 1947

Slide chart pubblicitaria per determinare i consumi di carburante, 1979
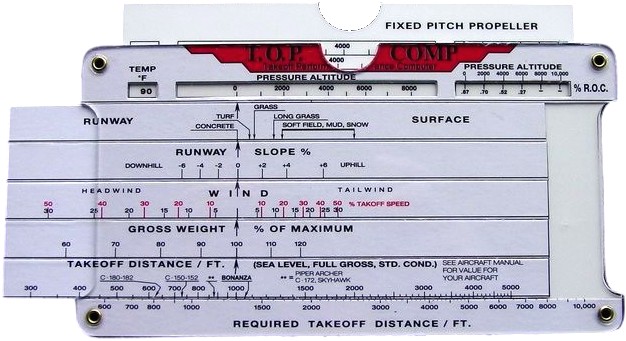
Il nomogramma di decollo inserito in una slide chart, 2010

Calcolatore per lavori di tornitura, 2020
Visitate la sezione dedicata alle slide chart per elettrotecnici
Le volvelle
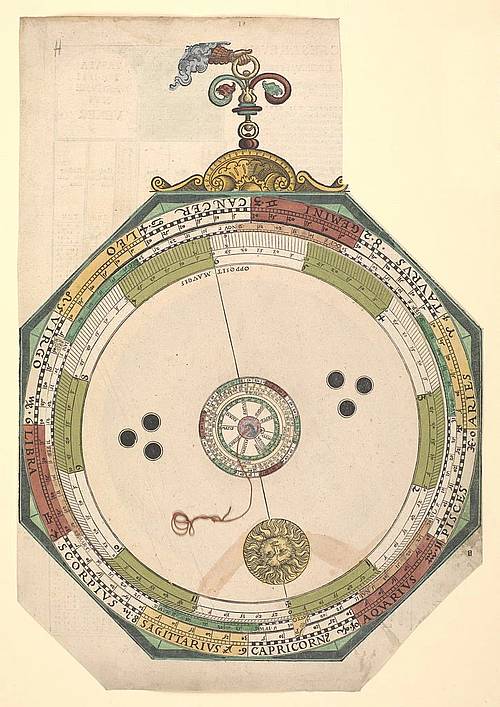
La "volvelle" è un antico sistemi per la previsione di eventi astronomici ciclici, prende il nome dal latino volvere (ruotare). E' infatti composta da un disco fisso sul quale ruotano uno o più dischi con stampate le scale o le informazioni da mettere in rapporto.
Matthew Paris, monaco benedettino inglese del 1200, fu il primo a integrare delle scale girevoli per calcolare la data della Pasqua nella sua opera Chronica Majora. Il sistema ebbe poi diffusione nel 1500 con il capolavoro di Petrus Appianus Astronomicum Caesareum, che presenta una serie di volvelle per prevedere le posizioni dei pianeti.
Le volvelle sono ideali per usi astronomici e sono preferite alle slide chart quando le scale circolari permettono una più facile lettura.
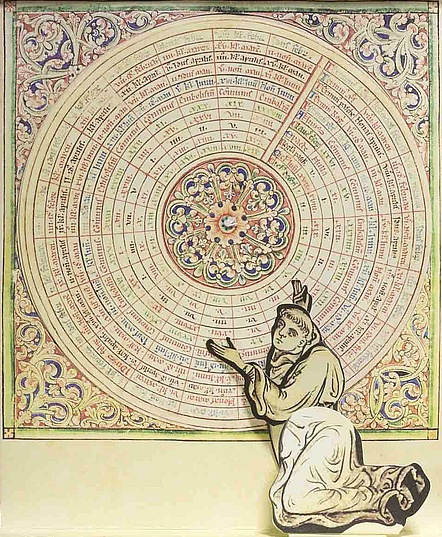
Paris Chronica Majora, 1245 e Apianus Astronomicum Caesareum, 1540

John Emslie Sheppard's Clock, 1844: le volvelle mostrano l'ora mondiale
e le costellazioni visibili in date e orari diversi


Volvelle medica e dimensionatore pannelli in masonite, 1945-55
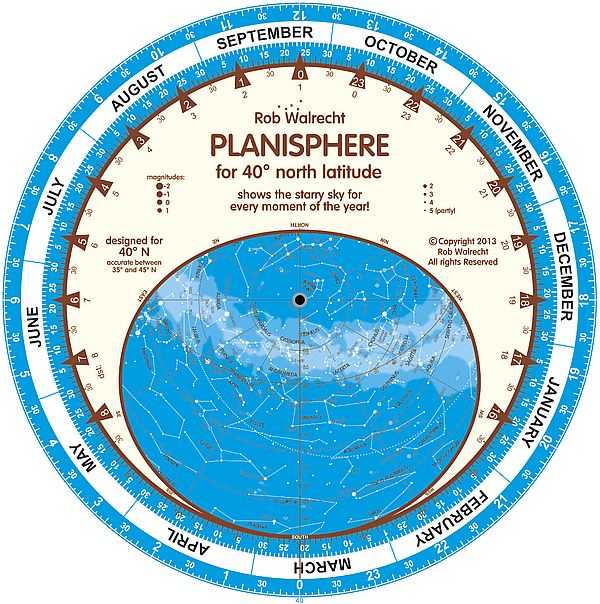
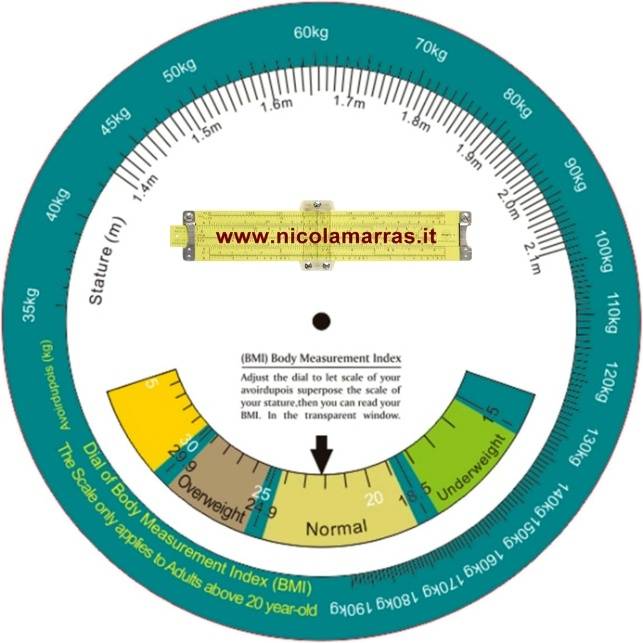
Volvelle astronomica e calcolatore della massa corporea, 2025
Un tempo i tecnici incontravano difficoltà nell'utilizzo dei regoli calcolatori, per i quali era necessaria una formazione da ingegnere. I metodi grafici permettono di visualizzare istintivamente le relazioni tra variabili e risolvere le equazioni anche senza conoscerle, impedendo errori grossolani.
Svolgevano la funzione delle moderne "app", chi è interessato può scaricare il classico testo First Course in Nomography e una collezione di nomogrammi storici di grande impatto visivo.
Altri nomogrammi, slide chart e testi scaricabili si trovano nella sezione dedicata ai calcolatori per elettrotecnici.
Links:
I Nomogrammi su Wikipedia
Slide chart su Wikipedia
Volvelle su Wikipedia
International Slide Rule Museum
La Nomografia su KASS
IREM La Reunion
Steve's Antique Technology
TakeOff Performance Computer
The Volvelle: a Smartphone App?
© 2004 - 2026 Nicola Marras Manfredi - IS1EH