Nepero e i logaritmi
John Napier, scoprendo i logaritmi, rivoluzionò il calcolo scientifico.
I logaritmi rimasero in uso per oltre 300 anni, permettendo i calcoli astronomici.
Il matematico John Napier (Nepero) sosteneva. "Eseguire dei calcoli è operazione difficile e lenta. La noia che ne deriva è la causa principale della disaffezione che la gente prova nei confronti della matematica". Trovò infine la soluzione nel 1614 con la scoperta dei logaritmi.
Questi, pubblicati nel "Mirifici logarithmorum canonis descriptio", sono in grado di esprimere qualsiasi numero positivo tramite potenze.
Il prodotto di due potenze con uguale base è una potenza con la stessa base ed esponente dato dalla somma degli esponenti.
Quindi coi logaritmi (dal greco logos e arithmos, cioè ragionamento coi numeri), moltiplicazioni e divisioni si possono effettuare come semplici addizioni e sottrazioni.
Napier introdusse inoltre l'uso della virgola nella notazione decimale.
Il calcolo scientifico nasce non a caso in Inghilterra.
La sua economia era legata alla navigazione, bisognava trovare strumenti adeguati per calcolare il punto nave.
Lo stesso impulso che le spedizioni spaziali diedero ai calcolatori elettronici.
In Spagna il problema era meno sentito in quanto le rotte per il Centroamerica si svolgevano per latitudine, necessitando di pochi calcoli.
Nel 1617 Henry Briggs, dopo diversi incontri con Napier, razionalizzò i logaritmi organizzandoli più praticamente in base 10 e stampandoli
in forma di tabelle, da lui chiamate "tavole".
Queste permettevano di calcolare fino alla quattordicesima cifra decimale.
Quanto una calcolatrice di oggi. In questa opera troviamo già il termine "mantissa" per le parti decimali, ma la prima esposizione sistematica è del 1742, con la pubblicazione della "Table of Logarithms" di William Gardiner.
Per moltiplicare due numeri basta cercare i loro logaritmi e sommarli. Otterremo il logaritmo del risultato. Consultando poi di nuovo le tavole lo trasformeremo nel risultato vero. In pratica il logaritmo di un numero in una certa base è l' esponente a cui bisogna innalzare la base per ottenere il numero stesso. Il logaritmo di 100 in base 10 è 2. (102 = 100). 10.000 x 1.000 si trasforma in. 104 x 103 = 104+3 = 107 = 10.000.000. Moltiplicando e dividendo gli esponenti troveremo inoltre i quadrati, i cubi e le relative radici.
Le cose si complicano quando trattiamo numeri diversi da 10 (es. il logaritmo di 2 è 0,301029, di 113 è 2,053078, di 1.415 è 3,150756 ecc.) ed occorrono tavole molto voluminose.
I logaritmi ebbero lunga vita. Erano economici e la loro precisione li rendeva indispensabili ad astronomi e naviganti.
Dal 1959 vennero elaborati al computer e le pubblicazioni cessarono solo attorno al 1975. Oggi i logaritmi si utilizzano principalmente per risolvere equazioni esponenziali.
Calcolare coi logaritmi è facile, compilare le tavole no. Molti scienziati e navigatori ringraziarono nei loro libri gli oscuri matematici che passarono la vita lavorando manualmente con grande fatica.

Due tavole della "Mirifici logarithmorum canonis descriptio", 1614
Calcolare coi logaritmi
Calcolare coi logaritmi è un procedimento meccanico che non impegna la mente ma utilizzare le tavole richiede molta pratica.
Proviamo ad eseguire 10,34 x 1.347.
Per prima cosa dobbiamo trovare il logaritmo di 10,34.
La tavola ci dà solo la parte decimale del logaritmo (mantissa).
La parte intera è data dalla potenza di dieci del numero, quindi 1.
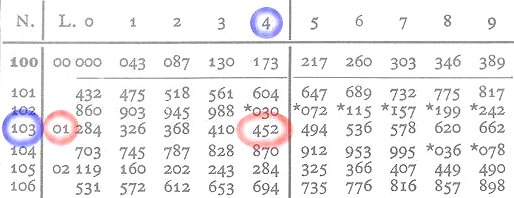
Per trovare la parte decimale togliamo la virgola al numero, che diventa 1034. La colonna N indica le prime 3 cifre. La quarta sarà nelle colonne numerate da 0 a 9.
Le prime due cifre della parte decimale si trovano nella colonna L in corrispondenza del 103 della colonna N (01). Le altre 3 cifre si trovano sulla stessa riga nella colonna del 4 (452). La parte decimale sarà quindi 01452. Il logaritmo completo 1,01452.
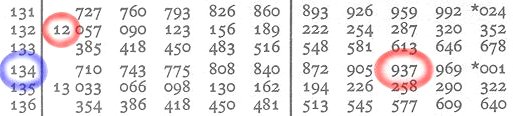
Ora, allo stesso modo, andremo in caccia del logaritmo di 1.347. La parte intera è 3 (10x10x10 = 1.000) e le prime 3 cifre 134. Sulla linea 134 manca il valore nella colon-na L e prenderemo l'ultimo valore prima della linea 134 (12). Le altre 3 si trovano sulla riga 134 di N nella colonna 7 (937). La parte decimale sarà quindi 12937. Il logaritmo completo 3,12937.
Adesso sommiamo il logaritmo di 10,34 al logaritmo di 1.347 (nel caso della divisione si deve sottrarre): 1,01452 + 3,12937 = 4,14389. Il prodotto tra 10,34 e 1.347 sarà il numero il cui logaritmo è 4,14389, cerchiamolo nelle tavole.
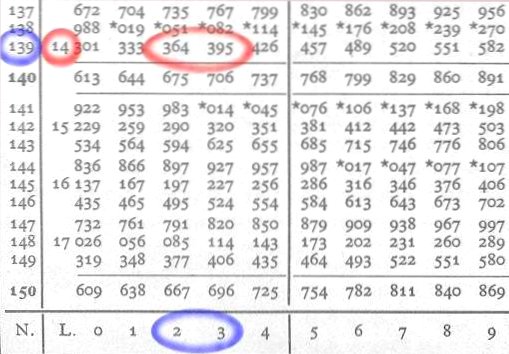
La parte intera del logaritmo è la potenza di 10 del numero cercato (4). Con la parte decimale (14389) troveremo le altre cifre.
La parte decimale inizia con le 2 cifre (14), le troviamo nella colonna L e poi cercheremo le altre 3 cifre (389) nelle colonne seguenti numerate da 0 a 9. Il 389 manca, ci sono invece il 364 nella colonna 2 ed il 395 nella colonna 3 della riga 139 di N. Il risultato sarà situato approssimativamente fra 13.920 e 13.930.
Per ottenere la quinta cifra esatta andremo ad interpolare con le tabelline P.P. (partes proportionales).
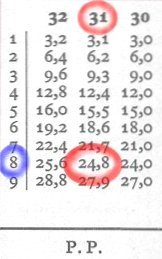
Dapprima dobbiamo trovare la differenza tra 395 e 364 (i 2 numeri alle colonne 2 e 3) 395 - 364 = 31 e consulteremo la tabella P.P. alla colonna 31. Poi cercheremo la differenza tra 389 (il valore non trovato) e 364 (il più piccolo dei 2 trovati. 389 - 364 = 25 guardando nella colonna 31 per il valore più vicino al 25 (24,8). Nella prima colonna in corrispondenza di 24,8 troviamo il numero 8 ed il risultato esatto sarà 13.928. Infatti 10,34 x1.347 = 13.928.
Oggi sembra un sistema poco pratico ma Nepero scriveva. "Ho cercato usando tutti i mezzi che avevo a disposizione e con le forze del mio intelletto di rendere più agevole e spedito il calcolo elaborando il metodo dei logaritmi a cui ho dedicato molti anni di studio". Un obbiettivo raggiunto. 200 anni più tardi Pierre-Simon de Laplace sosteneva ancora che "il lavoro di Napier ha raddoppiato la vita di noi astronomi".
Links:
I logaritmi su Wikipedia
I logaritmi su Edutecnica
© 2004 - 2026 Nicola Marras Manfredi - IS1EH
