Regolo calcolatore di carta        Regolo calcolatore virtuale

Utilizzare il regolo analogico

Il regolo calcolatore sostituisce le funzioni matematiche con misurazioni lineari analogiche.

Permette di: moltiplicare, dividere, elevare potenze, estrarre radici.

Questo è un breve tutorial, scaricate la versione integrale.

Vediamo come sommare, utilizzando due righelli graduati in centimetri:

Per eseguire 2 + 3 basta mettere lo 0 del righello B in corrispondenza del 2 del righello A, leggendo il risultato sul righello B sopra il 3:

Abbiamo quindi uno strumento in grado di effettuare addizioni. Per le sottrazioni basta invertire il procedimento: 6 - 4 = 2.

Dall'accuratezza della costruzione dipende la precisione dei risultati. Perà, anche dividendo ulteriormente le scale, non si riesce ad operare con numeri superiori a 100.
E' chiaro quindi che per quanto riguarda l'addizione e la sottrazione il regolo calcolatore è inferiore a qualsiasi altro tipo di calcolatrice.

Questo meccanismo diventa però potentissimo se le scale vengono disegnate utilizzando la successione logaritmica, posizionando cioè i numeri ad una distanza dall'origine proporzionale al valore del loro logaritmo. I logaritmi sono in grado di esprimere qualsiasi numero positivo tramite potenze.

Visto che il prodotto di due potenze con uguale base è una potenza con la stessa base ed esponente dato dalla somma degli esponenti, coi logaritmi moltiplicazioni e divisioni si possono effettuare come semplici addizioni e sottrazioni. Utilizzeremo il nuovo righello come il precedente.

Il logaritmo di un numero è l'esponente a cui bisogna innalzare la base per ottenere il numero stesso. I logaritmi si possono calcolare con qualsiasi base. Noi useremo la base 10 chiamata anche "log".

Il logaritmo di 10 in base 10 è 1 (10¹ = 10), di 10.000 è 4 (10⁴ = 10.000) e l'operazione 10 x 10.000 si trasforma in 10¹⁺⁴ = 10⁵ = 100.000.
Il logaritmo di un numero tra 1 e 10 è compreso tra 0 e 1. Es. il logaritmo di 2 è 0,301. Ecco la tabella:

Costruiamo ora la scala: l'1 è il punto di partenza, il 2 si trova a 3,01 cm, il 3 a 4,77 e cos via fino a 10. Possiamo quindi rappresentare ogni numero in quanto possiamo leggere, per esempio, il numero 3 anche come 30, 300, 0.003, 0.3, ecc.

Aggiungiamo le divisioni secondarie (logaritmi tra 1 e 99) e disegnamo il righello superiore. Il nostro regolo calcolatore è pronto:

Volendo eseguire 2 x 4 allineiamo l' 1 della scala B in corrispondenza del 2 della scala A. Leggeremo il risultato sulla scala A sopra il 4 della scala B.

Abbiamo adesso uno strumento in grado di effettuare moltiplicazioni.
L'immagine precedente mostra anche come eseguire 8/4: posizionare il 4 della scala B in corrispondenza dell' 8 della scala A. Leggeremo il risultato sulla scala A sopra l' 1 della scala B.

Il regolo ha dei limiti. Per calcolare 4 x 3 imposteremo i righelli nel modo seguente:

Ma, come appare nella figura, andiamo fuori scala. Occorre reimpostare l'operazione utilizzando il 10 della scala B e non l' 1:

In questo modo otteniamo 1,2 ma il risultato corretto è 12, non 1,2. Infatti il regolo restituisce solo le cifre, per gli zeri. Per posizionare la virgola bisogna sempre tenere presente il calcolo che si sta eseguendo.
Le cose sono più difficili volendo eseguire 1.237 x 23: bisogna infatti ridurre a 1,237 x 2,3 sforzandoci di approssimare con attenzione.

Esempi pratici

Sui regoli calcolatori le varie scale sono indicate da lettere: due sono le basiche, una sullo scorrevole (C) e una sul corpo (D). Le altre servono per semplificare i calcoli quando si è in presenza di quadrati e radici (A e B), cubi e radici cubiche (K), elevazione a potenza (LL), seni e tangenti (ST e T), moltiplicazione e divisione per pi (CI e CF), ecc.

Per cominciare useremo il semplice regolo di carta che potete stampare scaricando questo template, come cursore basterà una graffetta. Anche con uno strumento così basico si possono effettuare operazioni complesse. Tenere presente che, per esempio, i valori "0,9", "9", "90", "900", "9.000" si leggeranno sempre come "9" e dobbiamo quindi posizionare a mente virgole e decimali.

Moltiplicazione (scale C e D)

Esempio: 2.300 x 3.400

• posizionare l' 1 situato a sinistra della scala C sopra il 2,3 della scala D;
• posizionare il cursore a fianco del 3,4 della scala C;
• posizionare il cursore a fianco del 3,4 della scala C;
• sulla scala D, a fianco del cursore, troviamo un valore di poco superiore 7,8 e correggiamo a mente i decimali. L risposta corretta è 7.820.000.

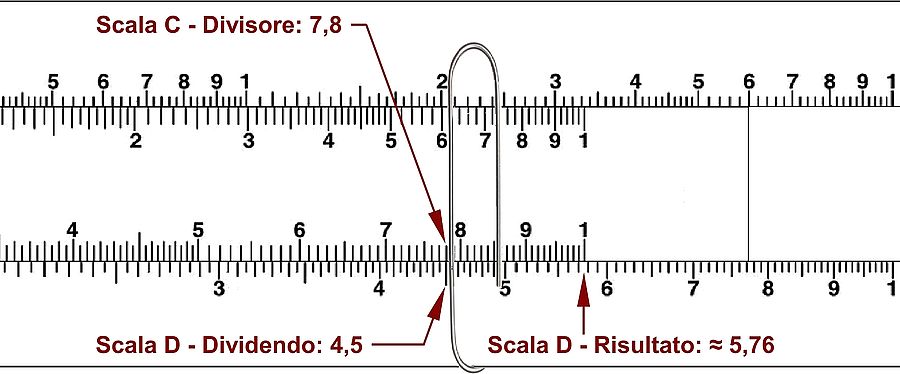
Divisione (scale C e D)

Esempio: 4.500 / 7.800

• posizionare il cursore a fianco di 4,5 sulla scala D
• posizionare il 7,8 della scala C a fianco del cursore;
• l' 1 situato a destra sulla scala C indica ca. 5,75 sulla scala D; posizioniamo a mente i decimali e otteniamo ca. 0,575. Il risultato esatto è 0,578.

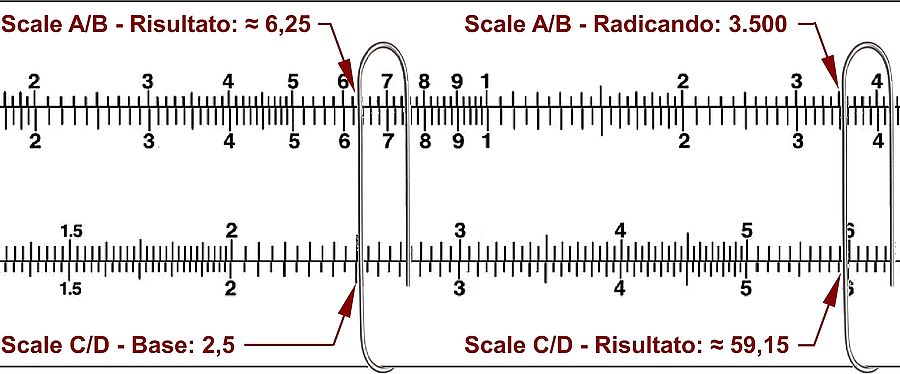
Quadrati e radici quadrate (scale A e D - B e C)

Esempio: 2,5²

• posizionare il cursore a fianco di 2,5 sulle scale C o D: il cursore è a fianco di 6,25 sulle scale A o B. Il risultato esatto è infatti 6,25.

Esempio: √3.500

• le scale A e B sono divise in due parti uguali: la metà sinistra serve per trovare la radice dei numeri con una quantità dispari di cifre, la metà destra quelli con un quantità pari.
• 3.500 ha un numero pari (4) di cifre ed utilizzeremo la metà destra. Spostando il cursore a fianco di 3,5 nelle scale A e D troviamo sulle scale C e D ca. 59,15. La radice esatta è 59,16.

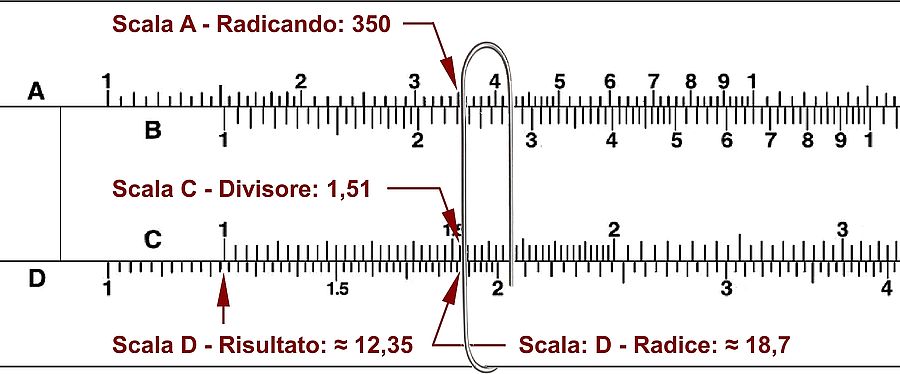
Eseguiamo ora una operazione più complessa: √350 / 1,51

• 350 è composto da un numero dispari (3) di cifre e quindi utilizzeremo la metà sinistra. spostando il cursore su 350 della scala A troviamo sulla scala D la sua radice quadrata:18,7;
• ora facciamo coincidere 1,51 della scala C sulla linea del cursore: sulla scala D, in corrispondenza dell' 1 sinistro dello scorrevole, leggiamo il risultato: 12,35.

Con una moderna calcolatrice saremmo stati più precisi, trovando 12,3896, ma questa piccola approssimazione non ha impedito a von Braun di inviare l'Uomo sulla Luna. Il regolo è infatti meno difficile di quanto sembri: il segreto sta nell'esercitarsi e un tempo lo trovava rapido e moderno. Come giudicheranno i nostri computer in futuro? Esercitatevi con questa simulazione del regolo calcolatore.

Links per apprendere il regolo calcolatore:

Il regolo calcolatore su Wikipedia
The Oughtred Society
Corso in inglese dello Slide Rule Museum
Tutorial in italiano su WikiHow

© 2004 - 2026 Nicola Marras Manfredi - IS1EH